
It started out with a question that has plagued physics for decades: whether the same mathematics could describe the jitter of subatomic particles and the sweep of galactic clusters. In recent research, Claudia Fevola of Inria Saclay and Anna‑Laura Sattelberger of the Max Planck Institute for Mathematics in the Sciences suggest that the solution might be found in an upstart field called positive geometry a system in which the universe’s most slippery processes are encoded, not in equations, but in the geometries of high‑dimensional spaces.
1. From Feynman Diagrams to Positive Geometry
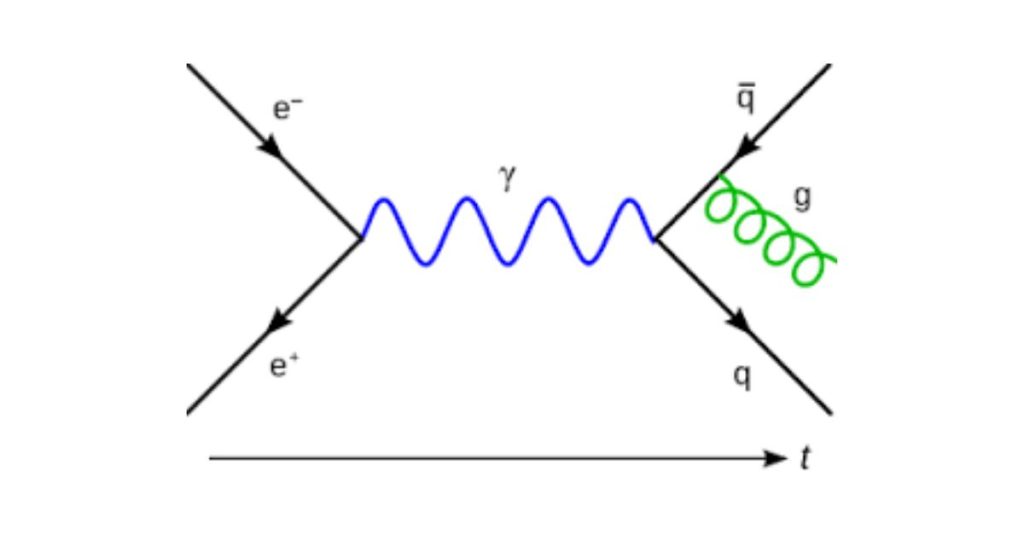
Since generations, Feynman diagrams have been the common language of quantum field theory, graphing particle interactions in networks of lines and vertices. Positive geometry does not abandon them but supplies a second perspective: interactions are now measurable volumes of geometric bodies like the amplituhedron, conceived by Nima Arkani‑Hamed and Jaroslav Trnka in 2013. In this method, the chance of a scattering process is derived from the volume of a sharply defined region in a higher-dimensional space, avoiding the combinatorial explosion of diagrammatic computation.
2. Generalizing Geometry to the Early Universe
The same geometric notions can also be brought to bear on cosmology. Cosmological polytopes positive geometries bespoke to the universe’s first light contain correlations in the cosmic microwave background. These shapes provide a concise summary of how quantum fluctuations in the early cosmos developed into today’s large-scale structure. As Daniel Baumann explained at a recent colloquium, Finding such structures is one of the central aims of the ERC Synergy Grant project UNIVERSE+.
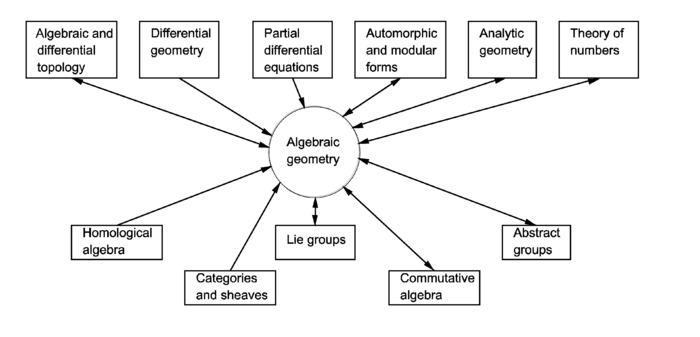
3. Algebraic Geometry as the Language of Unification
Central to this vision of unification is algebraic geometry, a discipline in which shapes are described by the solution sets of polynomial equations. In scattering theory, the graph polynomial of a Feynman diagram is constructed from the interaction graph’s spanning trees and forests. The corresponding Feynman integral can be written as a Mellin transform of a power of this polynomial, with physical kinematics constraining the coefficients. Such integrals are not mathematical curiosities they directly correspond to measurable quantities in collider experiments and cosmological surveys.

4. D‑Module Theory and Differential Equations
To master the intricacy of such integrals, scientists look to D‑module theory, which regards systems of linear differential equations as algebraic objects. Feynman integrals are reduced to pairings of twisted cycles with cocycles on algebraic varieties, and their analytic properties are codified by holonomic D‑modules. Formulating the explicit differential equations they obey often inverse images of hypergeometric D-modules is still a prominent technical challenge, but one that holds out hope for algorithmic breakthroughs in particle physics and cosmology.
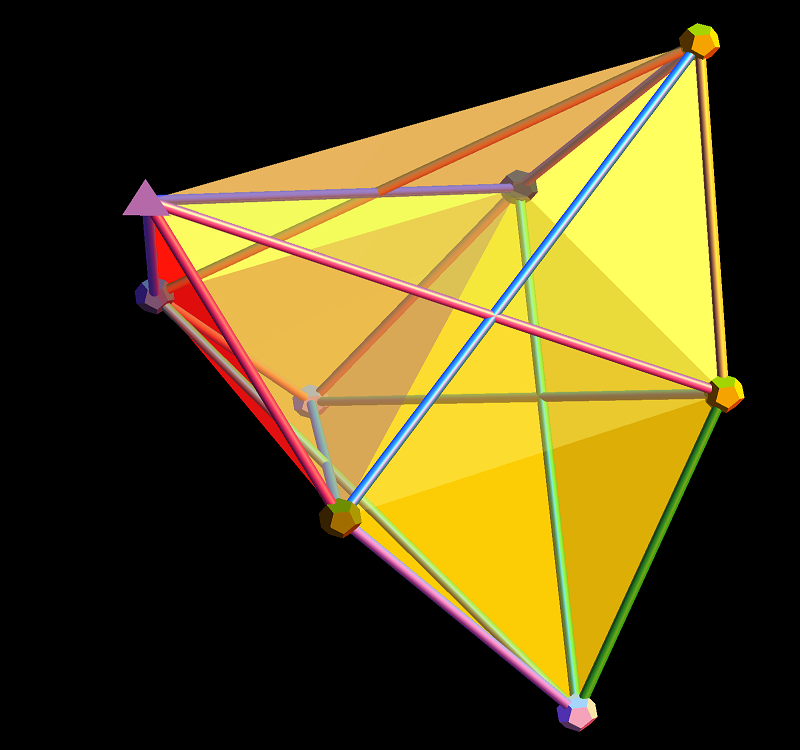
5. Combinatorics and the Geometry of Interactions
Amplituhedra or cosmological polytopes have rich combinatorial structure. Facets, edges, and vertices of amplituhedra or cosmological polytopes map to physical boundaries factorization channels in scattering amplitudes and the tilings map to the algebraic organization of interaction histories. Research in cluster algebras and Grassmannian tilings has uncovered emergent symmetries, suggesting that there are more fundamental organizing principles that may reduce calculations across very different physical regimes.
6. Master Integrals and Topology
An arresting connection between geometry and computation arises in the idea of master integrals: a minimum set of all integrals for a process. The number of master integrals, in general situations, is equal to the topological Euler characteristic with signs of the variety defined by the graph polynomial. This topological invariant hence prescribes the dimension of the space of independent physical quantities a connection between pure math and experimental observables.
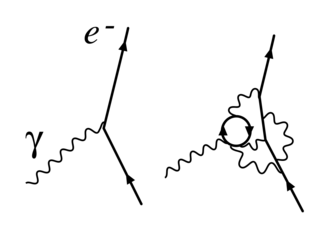
7. Renormalization in Geometric Terms
Recent developments reformulate renormalization group equations in geometric terms. For instance, in the Standard Model Effective Field Theory, curvature tensor evolution from combined metrics ( \bar{g} ) contains scale dependence of interaction strengths. At one loop, unitarity cuts of on-shell amplitudes directly contribute to flow of these geometric objects, providing a unified framework to monitor how physics varies with energy without having to go back to a reemergence of operator coefficients.

8. Beyond the Idealized Models
Most of today’s effort is in supersymmetric or flat‑spacetime models, where the mathematics is most manageable. Generalizing positive geometry to incorporate realistic aspects curved spacetimes, broken symmetries, non‑supersymmetric interactions is an open frontier. The UNIVERSE+ collaboration, spearheaded by Arkani‑Hamed, Baumann, Johannes Henn, and Bernd Sturmfels, is working on these generalizations in earnest, seeking to fold gravity and cosmic expansion into the same geometric structure that beautifully explains particle collisions.

The dream is grandiose: one geometric language that embodies the nature of phenomena from femtoscopic to intergalactic. In the words of Fevola and Sattelberger, “Positive geometry is a young science, but it can strongly impact basic research in physics as well as mathematics.” And if their instincts turn out to be correct, the next great unification in physics will perhaps not be inscribed in the notation of a Lagrangian, but in the faces and volumes of forms that extend across worlds infinitesimal and infinite.

