
A hundred years on from Einstein’s general relativity, the quantum of gravity is still one of physics’ greatest mysteries. And now, a new laboratory technique developed by a group led by Professor Johanna Erdmenger at the University of Würzburg allows the AdS/CFT correspondencea pillar of quantum gravityto be simulated using branched electrical circuits optimized with hyperbolic lattices. This method not only lays out new possibilities for exploring the structure of spacetime, but also suggests future technological breakthroughs in quantum signal communication in artificial intelligence.

1. The AdS/CFT Correspondence: Reconciling Gravity and Quantum Theory
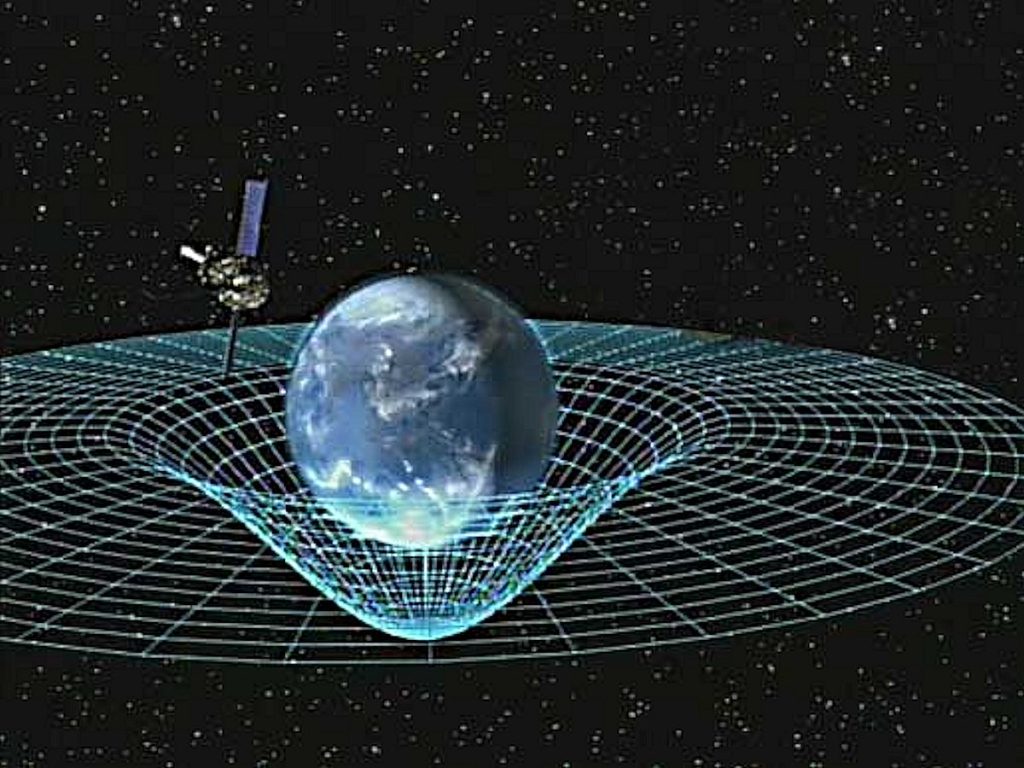
Quantum gravity research focuses on the so-called AdS/CFT correspondence-a duality positing a deep connection between gravitational theories in a high-dimensional, negatively curved spacetime (Anti-de Sitter, or AdS), and conformal field theories (CFT) defined on its lower-dimensional boundary. In this way, as Professor Erdmenger will explain, “The AdS/CFT correspondence allows us to understand difficult gravitational processes, such as those that exist in the quantum world, using simpler mathematical models.” At its heart is a curved spacetime, which can be thought of as a funnel.

The correspondence states that the quantum dynamics at the edge of the funnel must correspond to the more complex dynamics insidesimilar to a hologram on a banknote, which generates a three-dimensional image even though it is only two-dimensional itself. This duality, first formulated by Maldacena in 1997, has become a central theoretical tool for recasting quantum gravitational questions in a tractable field-theoretic language, offering a “holographic” map between bulk and boundary physics string theory on AdS space is dual to a 4D supersymmetric Yang-Mills CFT.
2. Hyperbolic Lattices: Engineering Curved Spacetime in the Lab
The challenge of realizing curved, negatively curved (hyperbolic) spaces in the laboratory is profound. Hilbert’s theorem asserts that the hyperbolic plane cannot be embedded in three-dimensional Euclidean space, making direct physical realization impossible. Yet, recent advances have enabled the emulation of such spaces through discretized networks. The Würzburg team’s approach leverages branched electrical circuits constructed as hyperbolic latticestessellations of regular polygons meeting at each vertex in a pattern that enforces negative curvature. In these circuits, each node represents a point in space, and the connectivity encodes the metric of the underlying hyperbolic geometry. As has been recently described in experimental work, “electric circuits enable time-resolved measurements, and signals in the present realization propagate along hyperbolic geodesics, a smoking gun signature of the negative curvature of space.”
3. Circuit Design: From Bloch-Wave Hamiltonians to Tunable Phase Elements
To simulate an infinite hyperbolic lattice in electric circuits, it is necessary to construct unit-cell circuits whose Laplacian mimics the tight-binding Hamiltonian of the hyperbolic crystal. The design incorporates tunable complex-phase elements, enabling the imprinting of Bloch phases along circuit edges. These phases can be adjusted by external voltages, offering unprecedented flexibility. The circuit Laplacian for each element is expressed as a matrix whose off-diagonal entries are controlled by the ratio of applied voltages, allowing the phase ϕ to be tuned continuously. This technical innovation means that the band structure and eigenmodes of the simulated “hyperbolic drum” can be probed directly, with the propagation of signals revealing the curvature-induced spectral reordering characteristic of hyperbolic geometry Bloch-wave Hamiltonians of hyperbolic lattices are equivalent to unit-cell circuits with tunable phases.

4. Laboratory Realization of Holographic Duality
The Würzburg group’s theoretical calculations demonstrate that in their branched circuit, the dynamics at the boundary of the mimicked spacetime correspond to those in the bulk, thus experimentally realizing a central prediction of the AdS/CFT correspondence. “A branched electrical circuit is used to mimic curved space-timethe electrical signals at the individual branch points of the circuit correspond to the gravitational dynamics that would be found at different points in space-time,” Erdmenger notes. Impedance measurements, voltage profiles, and time-resolved signal propagation in these circuits confirm that wavefronts travel along hyperbolic geodesics, and that the spectrum of eigenmodes matches the predictions of the Laplace-Beltrami operator on a hyperbolic disk spectral reordering is a universal feature of negative curvature.

5. Competing Quantum Simulation Platforms: Circuits, Photonics, and Superconductors
While electrical circuits offer flexibility and accessibility, other platforms for simulating AdS/CFT physics include superconducting circuits and photonic systems. Superconducting circuits can exploit quantum coherence and entanglement, allowing for the simulation of quantum field theories with fewer decoherence effects. Photonic lattices, on the other hand, can realize synthetic dimensions and topological phases. However, the topolectrical approach stands out for its ease of fabrication, tunability, and direct measurement capabilities, making it a leading candidate for experimental holography electric circuits excel in flexibility and measurement accessibility.

6. Quantum Circuits for Low-Loss Signal Transmission in AI
Beyond fundamental physics, the unique properties of hyperbolic quantum circuits have immediate technological implications. “Our circuits also open up new technological applications,” Erdmenger explains. “Based on quantum technology, they are expected to transmit electrical signals with reduced loss, since the simulated curvature of space bundles and stabilizes the signals. This would be a breakthrough for signal transmission in neural networks used for artificial intelligence, for example.” In conventional neural networks, signal degradation and crosstalk limit performance, especially as architectures scale. The hyperbolic geometry of these circuits focuses and stabilizes signals, potentially enabling the development of quantum neural networks with superior efficiency and resilience quantum neural networks exploit quantum states to encode and process information.

7. Toward Neuromorphic Quantum Architectures
The intersection of quantum information and neural computation is giving rise to neuromorphic quantum models, where quantum circuits emulate the parallelism and adaptability of biological brains. Quantum neural networks (QNNs) leverage superposition and entanglement to achieve exponential scalability in certain tasks, and the injection of hyperbolic circuit principles may open up new avenues for building even more powerful QNNs. As described in recent reviews, “QNNs could inspire new neuromorphic designs, employing quantum algorithms to model phenomena such as associative memory and probabilistic reasoning.”

The ability to implement tunable, low-loss, and topologically protected signal pathways in hardware could accelerate the development of uncertainty-aware, robust AI systems for high-stakes applications. The Würzburg team’s work marks a pivotal step in bringing the mathematics of quantum gravity into the laboratory, while simultaneously charting a course toward next-generation quantum technologies.

